中國粉體網(wǎng)訊 粉體顆粒概述
粉體顆粒一般認(rèn)為是由大量常規(guī)操作及分散條件下不可再分的固體顆粒聚集而成,其內(nèi)部存在大量空隙,屬于復(fù)雜的多相系統(tǒng),,如日常生活中常見的土壤、砂石、積雪等,。
粉體顆粒單獨(dú)來看是由小顆粒組成,既具備固體的抗變形能力等,,因此便于對粉體顆粒進(jìn)行進(jìn)一步的加工操作,;粉體作為聚集體,又具備了液體一樣的可流動性,,便于對其進(jìn)行運(yùn)輸,;同時粉體還具有氣體的可壓縮性及可分散性,這就使得粉體具有較大的比表面積,,從而能充分與周圍環(huán)境直接接觸,,可以增大比表面積,有助于促進(jìn)相關(guān)反應(yīng)的進(jìn)行,。因此也有學(xué)者認(rèn)為粉體是一種新的物質(zhì)形態(tài),。
目前針對粉體顆粒大小的劃分并不統(tǒng)一,一般可分為三類,。粒徑在20~200微米的顆粒稱為細(xì)粉,;粒徑在3~20微米的顆粒稱為微粉;3微米以下的顆粒稱為超細(xì)粉體,。
粉體壓縮基本理論
由于粉體顆粒的離散特性,,導(dǎo)致其在自然堆積狀態(tài)下體系內(nèi)部會存在一定的空隙,,使得粉體具有一定的可壓縮性。在外加負(fù)載作用下,,粉體能夠變得密實(shí)甚至被壓縮成具有一定形狀和強(qiáng)度的產(chǎn)品,。粉體這一壓縮變化過程,大體可以分為以下三個階段,。

顆粒所受壓力與密度變化曲線
初始階段,,受壓顆粒發(fā)生重新排列,受壓顆粒間會相互靠近使接觸面積增加,,大量顆粒會發(fā)生滑移,、轉(zhuǎn)動現(xiàn)象。這一過程會使被壓縮粉體原有的內(nèi)部穩(wěn)定結(jié)構(gòu)被破壞,,使得顆粒間原有的空隙在外力作用下由于顆粒間的移動,、旋轉(zhuǎn)等方式被極大縮小,重新排列成較為致密的充填結(jié)構(gòu),。這個階段主要特征是以顆粒重排為主,,粉體表觀密度隨壓力增加迅速增加。
第二階段,,被壓縮粉體密度隨壓力增加變化顯著減緩,。這一過程粉體顆粒間接觸面積進(jìn)一步增大,此時會給壓縮過程帶來一定阻力,,如顆粒間的摩擦力,、由于顆粒嚙合造成的機(jī)械結(jié)構(gòu)所導(dǎo)致的機(jī)械阻力等。
第三階段,,當(dāng)負(fù)載到達(dá)一定程度并且顆粒間接觸面積足夠大時,,粉體顆粒間的空隙已經(jīng)很難再被壓縮。此時繼續(xù)增大負(fù)載,,會在顆粒內(nèi)部引起顆粒的彈性變形和塑性變形,。當(dāng)壓力卸載后,能夠恢復(fù)的變形部分即為彈性變形,,不能恢復(fù)的變形部分為塑性變形,。如果繼續(xù)增大負(fù)載,此時顆粒會因?yàn)橥饬^大而發(fā)生破碎,,分裂成更多更小的粉體顆粒,。較小的破碎顆粒會進(jìn)入大顆粒的空隙內(nèi)。這一過程伴隨著顆粒間的變形與顆粒破碎,,將導(dǎo)致粉體密度隨著壓力變化繼續(xù)上升,。
總體來說,可將粉體壓縮過程總結(jié)為:第一階段粉體的壓縮以顆粒間的位移為主,;第二階段主要發(fā)生顆粒的加工硬化,;第三階段以顆粒受壓發(fā)生形變?yōu)橹鳌?/p>
粉體壓縮經(jīng)典方程
由于粉體在壓縮過程中所發(fā)生的機(jī)械嚙合,、彈性形變、塑性形變,、顆粒破碎等過程,,很難用單一的數(shù)學(xué)方程進(jìn)行解釋。因此研究者們嘗試使用壓縮過程中涉及的壓力與粉體床層固結(jié)狀態(tài)的性質(zhì)如孔隙率,,體積或密度,,來描述粉體壓縮過程,由此提出了多種用于描述粉體床層高度或體積變化與所施壓力之間函數(shù)關(guān)系的經(jīng)驗(yàn)公式,。
1923年,,Walker在研究金屬粉末壓縮過程中,提出了用于描述粉體體積變化與壓力之間關(guān)系的Walker方程:
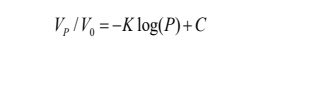
式中,,VP,V0分別為壓縮后粉體體積與空隙率為零時體積,,P為軸向壓力,,K,C為常數(shù),與粉體種類有關(guān),。Walker方程主要應(yīng)用于金屬粉體的相關(guān)研究中,,適用于高壓條件下粉體壓縮行為的有關(guān)研究。
1961年,,Heckel基于一級化學(xué)反應(yīng)動力方程的假說將濃度和時間替換為孔隙率和壓力,,提出了可應(yīng)用于描述金屬及非金屬粉體孔隙率與壓力之間關(guān)系的Heckel方程:
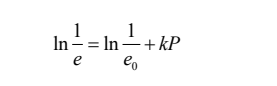
式中,e0,,e分別為粉體自然狀態(tài)下的空隙率與壓力為P時的空隙率,,k為常數(shù),可以用來衡量粉體的可壓縮性,。Heckel方程是藥物粉體壓縮領(lǐng)域中常用的經(jīng)驗(yàn)公式,,用于描述粉體的相對密度與施加壓力的變化關(guān)系。但有關(guān)文獻(xiàn)指出,,在較低壓力和較高壓力下,,該方程存在一定誤差,只有在中間壓力階段呈線性關(guān)系,。
1971年,,川北公夫根據(jù)陶瓷粉體的壓縮規(guī)律,推導(dǎo)出粉體的相對體積與壓力之間的Kawakita方程:
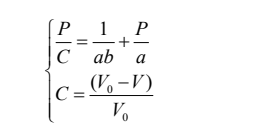
其中a和b均為常數(shù),,a是在壓強(qiáng)P下粉體體積減小量,,用于描述粉體的壓縮性質(zhì)。V0是粉體自然堆積狀態(tài)下體積,,V是在壓強(qiáng)P下粉體壓縮后的體積,,C為粉體壓縮前后體積變化率,。Kawakita方程是在藥物粉體壓制成型中最常見的經(jīng)驗(yàn)方程,并且川北方程還可以適用于粉體等靜壓成形,、沖擊成形等不同方式的壓縮過程中,,其適用于柔軟松散即低壓條件和高孔隙率的粉體壓縮研究。
1980年,,黃培云結(jié)合粉體壓縮過程中會出現(xiàn)加工硬化的現(xiàn)象,,并引入了時間因素對粉末壓縮的影響,提出了雙對數(shù)壓制方程:
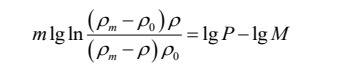
式中,,ρ為壓縮后粉體密度,;ρ0為粉體松裝密度;ρm為材料的理論密度,;P為所用壓強(qiáng),;M為壓制模量;m為加工硬化指數(shù),,用來表征粉體壓縮的難易程度,。該方程在金屬粉末冶金領(lǐng)域中得到了廣泛應(yīng)用,適用于硬質(zhì)金屬粉體的成型研究,。
參考來源:
霍楓.粉體離心壓縮過程仿真與動力學(xué)分析
(中國粉體網(wǎng)編輯整理/青黎)
注:圖片非商業(yè)用途,,存在侵權(quán)告知刪除


















